Реципрочното или реципрочното е много полезно при всички видове алгебрични уравнения. Например, когато разделяте една дроб на друга, умножавате първата дроб по реципрочната стойност на втората. Когато търсите уравнението на линия, трябва да използвате и обратното.
Стъпка
Метод 1 от 3: Намиране на обратната част на дроб или цяло число
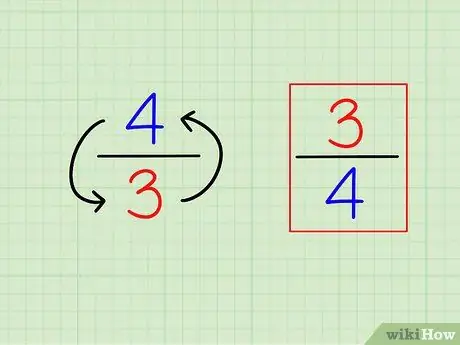
Стъпка 1. Намерете реципрочната стойност на дробата, като я обърнете
Определението за „реципрочно“или обратното е много лесно. За да намерите реципрочното на всяко цяло число, просто изчислете "1 (това число)". За дроби реципрочната е различна дроб, тоест числата са „обърнати“(обратно).
- Например обратното на 3/4 е 4/3.
- Всяко число, умножено по неговата реципрочна възвръщаемост 1.
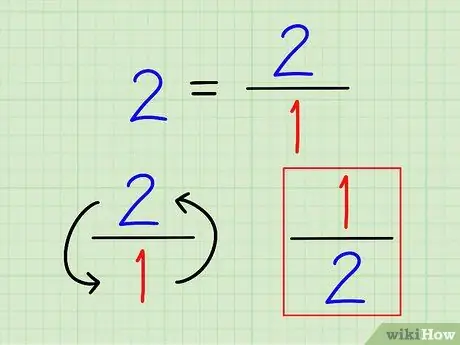
Стъпка 2. Напишете реципрочната стойност на цялото число като дроб
Отново реципрочното число винаги е 1 (това число). За цели числа ги запишете като дроби. Няма смисъл да се изчислява това число до десетична запетая.
Например реципрочното на 2 е 1 2 = 1/2.
Метод 2 от 3: Намиране на обратната част на смесена дроб
Стъпка 1. Определете смесени числа
Смесените дроби се състоят от цели числа и дроби, като 24/5. Има две стъпки за намиране на реципрочността на смесено число, както е описано по -долу.
Стъпка 2. Преобразувайте смесените числа в неправилни дроби
Не забравяйте, че 1 винаги може да бъде записано като (число)/(същото число), а дроби със същия знаменател (най -долния номер) могат да се добавят заедно. Ето пример за използване на 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
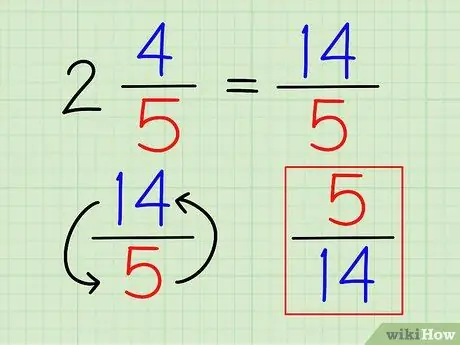
Стъпка 3. Обърнете фракцията
След като числото е изписано изцяло като дроб, можете да намерите неговата реципрочност, точно както бихте направили всяка друга дроб, като обърнете дроб.
В горния пример реципрочното на 14/5 е 5/14.
Метод 3 от 3: Намиране на противоположността на десетичен знак
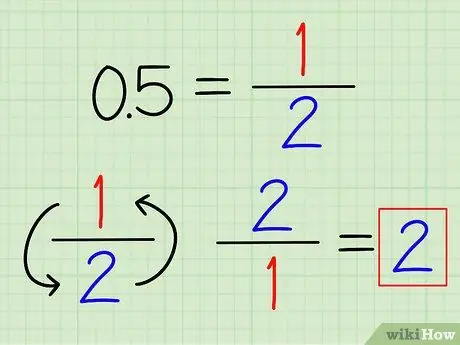
Стъпка 1. Преобразувайте десетичните числа в дроби, ако е възможно
Може да разпознаете някои често използвани десетични числа, които лесно могат да бъдат преобразувани в дроби. Например 0,5 = 1/2 и 0,25 = 1/4. След като десетичната запетая е преобразувана в дроб, просто обърнете дробта, за да намерите нейната реципрочност.
Например реципрочната стойност от 0,5 е 2/1 = 2.
Стъпка 2. Напишете задача за разделяне
Ако не можете да го преобразувате в дроб, изчислете реципрочната стойност на числото под формата на задача за деление: 1 (десетична). Можете да използвате калкулатор, за да го разрешите или да преминете към следващата стъпка, за да го разрешите ръчно.
Например, можете да намерите реципрочната стойност на 0.4, като изчислите 1 0.4
Стъпка 3. Променете задачата за разделяне, за да използвате цели числа
Първата стъпка към разделянето на десетичните знаци е да преместите десетичната запетая, докато всички числа са цели числа. Докато премествате десетичната запетая на двете числа с еднакъв брой стъпки, ще получите правилния отговор.
Например, можете да използвате 1 0, 4 и да го пренапишете като 10 4. В този случай премествате всички десетични знаци с една стъпка надясно, по същия начин, по който умножавате всяко число по десет
Стъпка 4. Решете проблема, като използвате дълго деление
Използвайте метода на дългото разделяне, за да изчислите реципрочното. Ако броите 10 4, ще получите отговора 2, 5 което е реципрочното на 0, 4.
Съвети
- Отрицателната реципрочност на числото е същата като обикновената реципрочна, като се умножава по отрицателна. Например отрицателната реципрочност на 3/4 е -4/3.
- Реципрочното или реципрочното често се нарича "обратно умножение".
- Числото 1 е обратното на себе си, защото 1 1 = 1.
- Числото 0 няма реципрочно, защото 0 е неопределено.
