Разделянето на дроби на цели числа не е толкова трудно, колкото изглежда. За да разделите дроб на цяло число, всичко, което трябва да направите, е да преобразувате цялото число в дроб, да намерите реципрочната стойност на дробта и да умножите резултата с първата дроб. Ако искате да знаете как да го направите, просто следвайте тези стъпки:
Стъпка
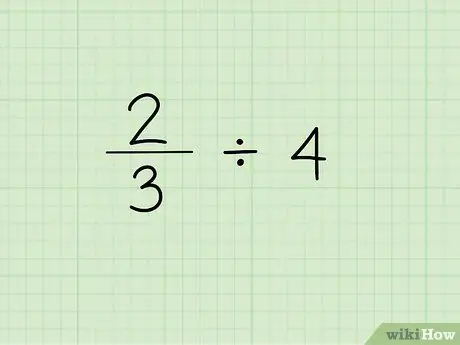
Стъпка 1. Запишете проблема
Първата стъпка към разделянето на дроб на цяло число е да напишете дроб, последвана от знака за разделяне и цялото число, от което се нуждаете, за да разделите дробата. Да речем, че работим със следния проблем: 2/3 4.
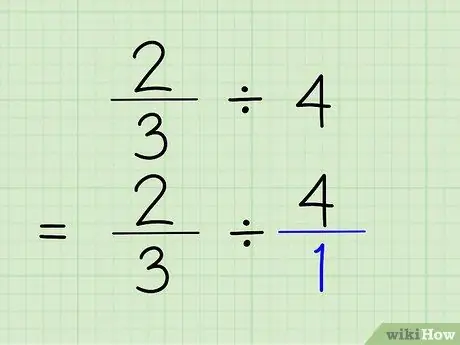
Стъпка 2. Преобразувайте цели числа в дроби
За да преобразувате цяло число в дроб, всичко, което трябва да направите, е да поставите цялото число над числото 1. Цялото число се превръща в числител, а 1 в знаменател на дроб. Да кажеш 4/1 наистина е същото като да кажеш 4, защото показваш само, че числото съдържа „1“4 пъти. Проблемът ще бъде 2/3 4/1.
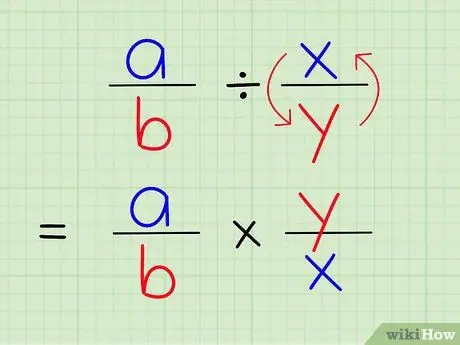
Стъпка 3. Разделянето на част от друга е същото като умножаването на тази дроб по реципрочната стойност на друга дроб
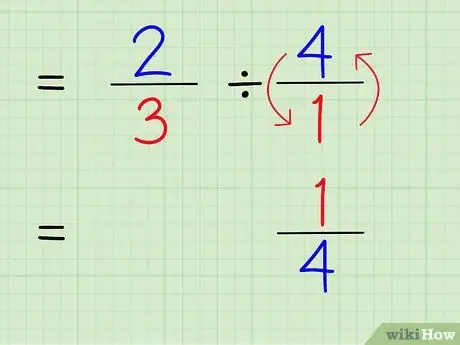
Стъпка 4. Напишете реципрочната стойност на цяло число
За да намерите реципрочното число, сменете числителя и знаменателя на числото. Следователно, за да намерите реципрочното на 4/1, просто разменете числителя и знаменателя, така че числото да стане 1/4.
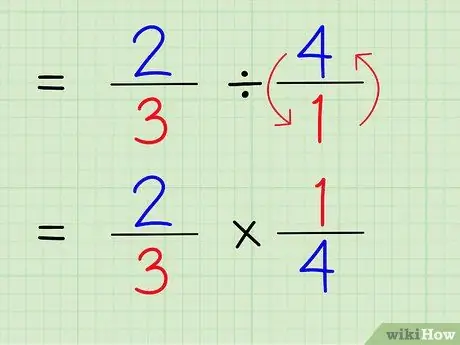
Стъпка 5. Променете знака за деление на знака за умножение
Проблемът ще бъде 2/3 x 1/4.
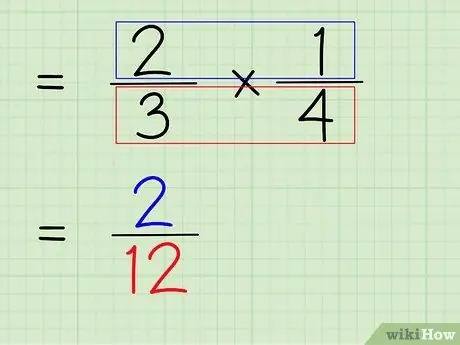
Стъпка 6. Умножете числителя и знаменателя на дробата
И така, следващата стъпка е да умножите числителя и знаменателя на дробата, за да получите нов числител и знаменател като краен отговор.
- За да умножите числителите, просто умножете 2 x 1, за да получите 2.
- За да умножите знаменателите, просто умножете 3 x 4, за да получите 12.
- 2/3 x 1/4 = 2/12
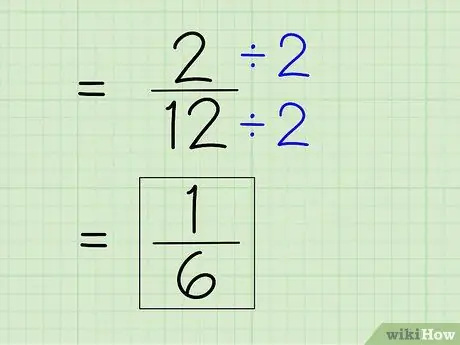
Стъпка 7. Опростете дробата
За да опростите дроб, трябва да намерите най -малкия знаменател, което означава, че трябва да разделите числителя и знаменателя на всяко число, което дели и двете числа. Тъй като 2 е числителят, ще трябва да видите дали 2 може напълно да раздели 12 - може, защото 12 е четно число. След това разделете числителя и знаменателя на 2, за да получите нов числител и знаменател, за да получите прост отговор.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Фракцията 2/12 може да бъде опростена до 1/6. Това е вашият окончателен отговор.
Съвети
- Това е за подпомагане на паметта, лесен начин да запомните как да направите всички тези изчисления. Имайте предвид това: "Лесно е да разделите дроби, да обърнете второто число и да умножите!"
- Друг вариант на горния метод е JGB/JBG. Не променяйте първия номер. Промяна на умножение. Обърнете последното число. Или първо B, след това G.
- Ако отмените изчислението, преди да го умножите, може да не се наложи да намерите най -простата форма на дробата, тъй като резултатът вече е в най -простата форма на дроб, както можете да видите. В нашия пример, преди да умножим 2/3 × 1/4, можем да видим, че първият числител (2) и вторият знаменател (4) имат същия множител 2, който можем да отменим, преди да продължим изчислението. Това преобразува проблема в 1/3 × 1/2, което дава незабавен резултат 1/6 и ни спестява време за опростяване на дробата на по -късен етап.
- Ако една от вашите дроби е отрицателна, този метод все още е работещ; не забравяйте да следите знаците, докато изпълнявате тези стъпки.
