- Автор Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:09.
- Последно модифициран 2025-01-23 12:07.
Разделянето на дроб на дроб в началото може да изглежда объркващо, но всъщност е наистина лесно. Всичко, което трябва да направите, е да обърнете, умножите и опростите! Тази статия ще ви преведе през процеса и ще ви покаже колко лесно е да разделите дроб на дроб.
Стъпка
Част 1 от 2: Разбиране на начина на разделяне на дроби на дроби
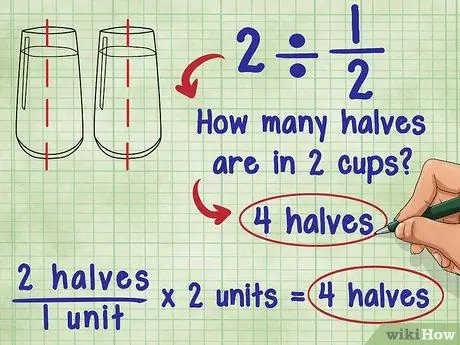
Стъпка 1. Помислете какво означава разделяне на дроб
относно 2 ÷ 1/2 попита Ада: "Колко половината са в 2?" Отговорът е 4, защото всяка единица (1) се състои от две „половини“и има 2 общи единици: 2 „половина“/1 единица * 2 единици = 4 „половина“.
- Опитайте да си представите същото уравнение с помощта на чаша вода: Колко и половина чаши вода има в 2 чаши вода? Можете да излеете 2 чаши и половина вода във всяка чаша вода. Това означава, че по принцип добавяте „половината“чаши вода и имате две чаши: 2 „половин“/1 чаша * 2 чаши = 4 „половина“.
- Това означава, че ако дробът, който разделяте, е между 0 и 1, отговорът винаги е по -голям от първоначалното число! Това е вярно, когато разделите цяло число или дроб на дроб.

Стъпка 2. Разберете, че разделянето е обратното на умножението
По този начин разделянето на дроб може да бъде решено чрез умножение по реципрочното на дробата. Реципрочното на дроб (наричано още „обратно умножение“) е дробът, който е обърнат, така че числителят и знаменателят да разменят местата. След малко ще разделим дробите на дроби, като намерим реципрочната стойност на втората дроб и умножим двете дроби. Нека обаче първо разгледаме някои от противоположностите:
- Реципрочното на 3/4 е 4/3.
- Обратното на 7/5 е 5/7.
- Реципрочното на 1/2 е 2/1 или 2.
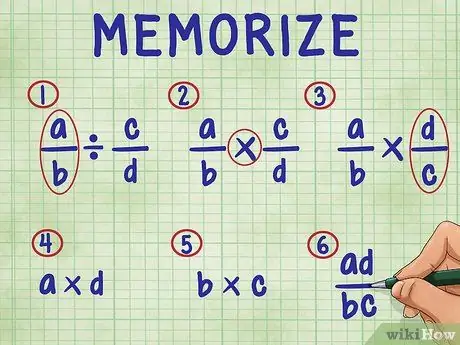
Стъпка 3. Запомнете следните стъпки, за да разделите дроб на дроб
По ред стъпките включват:
- Просто оставете първата дроб в уравнението.
- Променете знака за деление на знака за умножение.
- Обърнете втората дроб (намерете нейната реципрочност).
- Умножете числителя (горния номер) на двете дроби. Резултатът от умножението е числителят (отгоре) на вашия отговор.
- Умножете знаменателя (долния номер) на двете дроби. Продуктът на продукта е знаменателят на вашия отговор.
- Опростете дробите си, като ги опростите до най -простите им условия.
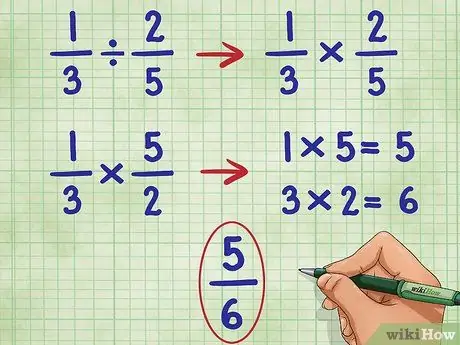
Стъпка 4. Изпълнете тези стъпки за примера 1/3 2/5
Ще започнем, като изоставим първата дроб и преобразуваме знака за деление в знак за умножение:
- 1/3 ÷ 2/5 = Става:
- 1/3 * _ =
- Сега обръщаме втората дроб (2/5), за да намерим нейната реципрочност, която е 5/2:
- 1/3 * 5/2 =
- Сега умножете числителя (горния номер) на двете дроби, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Сега умножете знаменателя (долния номер) на двете дроби, 3*2 = 6.
- Сега имаме: 1/3 * 5/2 = 5/6
- Тази дроб не може да бъде опростена допълнително, затова имаме нашия отговор.

Стъпка 5. Опитайте се да запомните следните рими, които да ви помогнат да запомните:
"Разделянето на дроби е лесно, обърнете втората дроб, след това умножете. Не забравяйте да опростите, преди да е време за ядене."
Друга полезна помощ за напомняне ви казва какво да правите с всяка част от уравнението: „Позволи ми (първа дроб), Промени ме (знак за разделяне), Обърни ме (втора дроб).“
Част 2 от 2: Разделяне на дроби по дроби в задачи
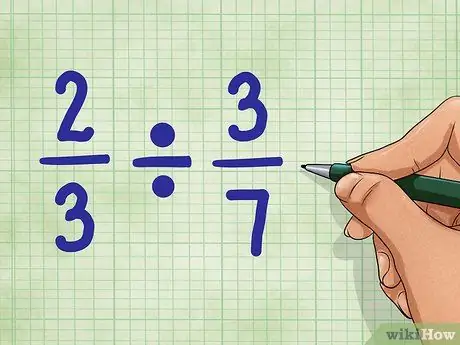
Стъпка 1. Започнете с примерни въпроси
Нека използваме 2/3 ÷ 3/7. Този въпрос изисква броя на частите, равен на 3/7, който може да бъде намерен в стойността 2/3. Не се безпокой. Не е толкова трудно, колкото звучи!
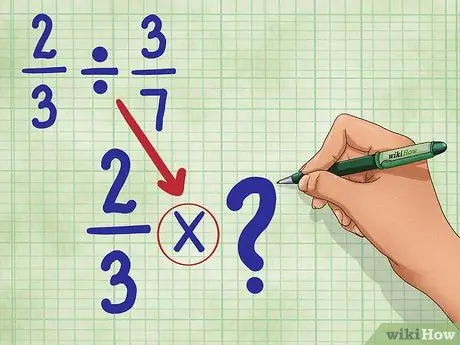
Стъпка 2. Преобразувайте знака за деление в знак за умножение
Вашето ново уравнение ще бъде: 2/3 * _ (След малко ще запълним това празно място.)
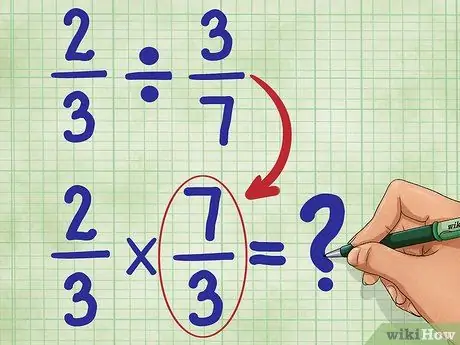
Стъпка 3. Сега намерете реципрочността на втората дроб
Това означава да обърнете 3/7, така че числителят (3) сега да е най -отдолу, а знаменателят (7) да е отгоре. Реципрочното на 3/7 е 7/3. Сега напишете новото си уравнение:
2/3 * 7/3 = _

Стъпка 4. Умножете дробите си
Първо умножете числителите на двете дроби: 2 * 7 = 14. 14 е числителят (горният номер) на вашия отговор. След това умножете знаменателите на двете дроби: 3 * 3 = 9. 9 е знаменателят (долният номер) на вашия отговор. Сега знаете това 2/3 * 7/3 = 14/9.
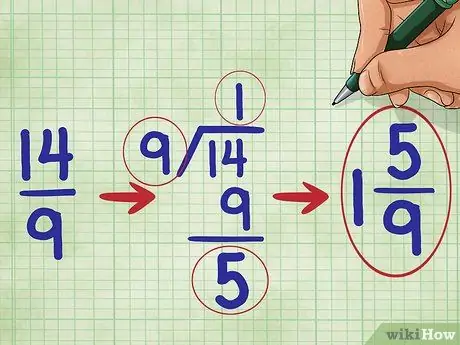
Стъпка 5. Опростете своята дроб
В този проблем, тъй като числителят на дробата е по -голям от знаменателя, ние знаем, че нашата дроб е по -голяма от 1. Трябва да я преобразуваме в смесено число. (Смесеното число е цяло число и дроб, комбинирани, например 1 2/3.))
-
Първо разделете числителя
Стъпка 14. с 9.
Числото 14, разделено на 9, е равно на едно с остатък от 5, така че трябва да запишете опростената си дроб като: 1 5/9 („Една пет-девета“).
- Спрете, вие сте намерили отговора! Можете да посочите, че вече не можете да опростявате дробата, тъй като знаменателят не се дели на числителя (9 не се дели на 5), а числителят е просто число или цяло число, което се дели само на едно и самото число.
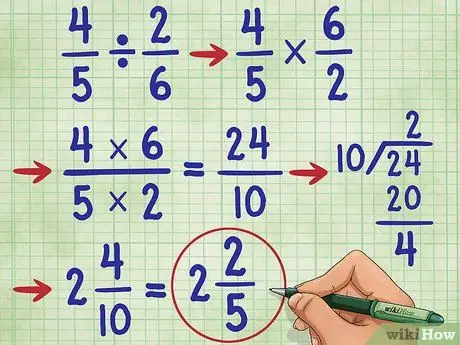
Стъпка 6. Опитайте друг пример
Нека опитаме въпроса 4/5 ÷ 2/6 =. Първо променете знака за деление на знака за умножение (4/5 * _ =), след това намерете реципрочното на 2/6, което е 6/2. Сега имате уравнението: 4/5 * 6/2 =_. Сега умножете числителя, 4 * 6 = 24, и знаменателя 5* 2 = 10. Сега имате 4/5 * 6/2 = 24/10.
Сега опростете дробата. Тъй като числителят е по -голям от знаменателя, трябва да преобразуваме тази дроб в смесено число.
- Първо разделете числителя на знаменателя, (24/10 = 2 останали 4).
- Напишете отговора като 2 4/10. Все още можем да опростим тази дроб отново!
- Обърнете внимание, че 4 и 10 са четни числа. И така, първата стъпка към опростяването му е да разделим всяко число на 2. Получаваме 2/5.
- Тъй като знаменателят (5) не се дели на числителя (2) и 5 е просто число, знаем, че тази дроб не може да бъде опростена допълнително. И така, нашият отговор е: 2 2/5.

Стъпка 7. Получете допълнителна помощ за опростяване на дробите
Вероятно сте прекарали много време да се научите как да опростявате дроби, преди да се опитате да ги разделите помежду си. Ако обаче имате нужда от опресняване или друга помощ, има някои страхотни онлайн статии, които могат да ви бъдат от голяма полза.
Свързани wikiHow статии
- Преобразуване на обикновени дроби в десетични знаци
- Изчисляване на площта на кръг
- Разделяне на полиноми с помощта на синтетично деление
- Разделяне на смесени дроби






