- Автор Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 10:56.
- Последно модифициран 2025-01-23 12:07.
Добавянето на дроби е много полезно знание. Това умение е много лесно за усвояване и използване при работа по математически задачи от началното до гимназията. Тази статия обяснява как да добавите дроби, така че да можете да го направите само за няколко минути.
Стъпка
Метод 1 от 2: Добавяне на дроби със същия знаменател

Стъпка 1. Проверете знаменателя (числото под частното) на всяка дроб
Ако числата са еднакви, тогава добавяте дроби със същия знаменател. Ако знаменателите са различни, прочетете втория метод.
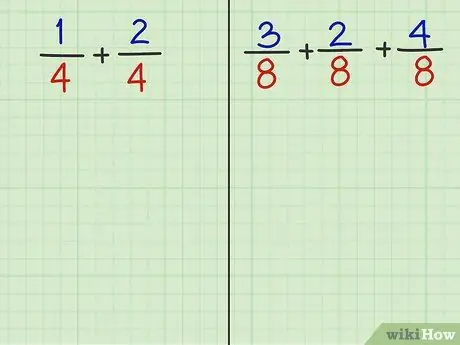
Стъпка 2. Отговорете на следните 2 въпроса
Четейки последната стъпка в този метод, трябва да можете да съберете частите от следните два въпроса.
- Проблем 1: 1/4 + 2/4
- Задача 2: 3/8 + 2/8 + 4/8
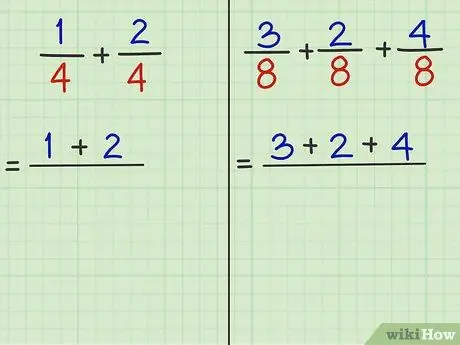
Стъпка 3. Съберете числителите (числата над делението) и ги съберете
Числителят е числото над частното. Без значение колко дроби искате да добавите, можете да добавите числителите веднага, ако знаменателите са еднакви.
- Проблем 1: 1/4 + 2/4 е фракцията, която трябва да се добави. "1" и "2" са числители. И така, 1 + 2 = 3.
- Задача 2: 3/8 + 2/8 + 4/8 е фракцията, която трябва да се добави. "3" и "2" и "4" са числители. И така, 3 + 2 + 4 = 9.

Стъпка 4. Определете новата дроб от сумата
Запишете числителя, получен в стъпка 2. Това число е нов числител. Напишете знаменателя, който е същото число под бисектрисата на всяка дроб. Не е нужно да правите изчисленията, ако знаменателите са еднакви. Този номер е нов знаменател и винаги се равнява на стария знаменател, когато добавяте дроби със същия знаменател.
- Проблем 1: 3 е новият числител и 4 е новият знаменател. По този начин отговорът на въпрос 1 е 3/4. 1/4 + 2/4 = 3/4.
- Задача 2: 9 е новият числител и 8 е новият знаменател. По този начин отговорът на въпрос 2 е 9/8. 3/8 + 2/8 + 4/8 = 9/8.
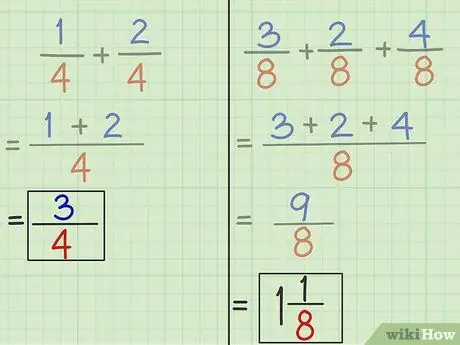
Стъпка 5. Опростете дробите, ако е необходимо
Не забравяйте да опростите новата дроб, за да улесните писането.
-
Ако числителят по -голям вместо знаменател като резултата от добавянето на задача 2, това означава, че получаваме 1 цял месец след опростяване на дробата. Разделете числителя на знаменателя или 9, разделен на 8. Резултатът е цяло число 1, което остава 1. Запишете цели числа пред дроб и остатъкът става числител на нова дроб със същия знаменател.
9/8 = 1 1/8.
Метод 2 от 2: Добавяне на дроби с различни знаменатели

Стъпка 1. Проверете знаменателя (числото под частното) на всяка дроб
Ако знаменателите са различни, вие сте добавете дроби с различни знаменатели. Прочетете следните стъпки, защото трябва да направите знаменателите равни, преди да добавите дроби.
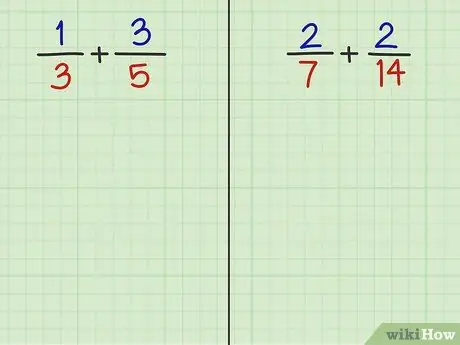
Стъпка 2. Решете следните 2 въпроса
Четейки последната стъпка в този метод, трябва да можете да съберете частите от следните два въпроса.
- Задача 3: 1/3 + 3/5
- Въпрос 4: 2/7 + 2/14

Стъпка 3. Съпоставете знаменателите
За да направите това, умножете знаменателите на двете дроби по -горе. Лесен начин за изравняване на знаменателите е да умножите знаменателите на двете дроби. Ако един от знаменателите е кратен на другия, намерете най -малкото общо кратно на двата знаменателя.
-
Проблем 3:
3 x 5 = 15. И така, новият знаменател на двете дроби е 15.
-
Проблем 4:
14 е кратно на 7. Следователно, трябва само да умножим 7 по 2, за да получим 14. Така новият знаменател на двете дроби е 14.

Стъпка 4. Умножете числителя и знаменателя на първата дроб с знаменателя на втората дроб
Тази стъпка не променя стойността на дробата, но дробът се променя, за да съответства на знаменателя. Дробната стойност остава същата.
-
Проблем 3:
1/3 x 5/5 = 5/15.
-
Проблем 4:
За този проблем просто трябва да умножим първата дроб на 2/2, за да получим знаменателите равни.
2/7 x 2/2 = 4/14

Стъпка 5. Умножете числителя и знаменателя на втората дроб с знаменателя на първата дроб
Подобно на стъпките по -горе, ние не променяме стойността на дробата, но дробът се променя, за да изравни знаменателя. Дробната стойност остава същата.
-
Проблем 3:
3/5 x 3/3 = 9/15.
-
Проблем 4:
Не е нужно да умножаваме втората дроб, защото знаменателите са еднакви.

Стъпка 6. Напишете двете нови дроби по ред
Към този момент не сме добавили двете дроби заедно, въпреки че можем. В горната стъпка умножихме всяка дроб по 1. Сега искаме да се уверим, че дробите, които искаме да добавим, имат един и същ знаменател.
-
Проблем 3:
вместо 1/3 + 3/5, дробът става 5/15 + 9/15
-
Проблем 4:
Вместо 2/7 + 2/14, дробът става 4/14 + 2/14

Стъпка 7. Добавете числителите на двете дроби заедно
Числителят е числото над частното.
-
Проблем 3:
5 + 9 = 14. 14 е новият числител.
-
Проблем 4:
4 + 2 = 6. 6 е новият числител.

Стъпка 8. Напишете общия знаменател (в стъпка 2) под новия числител или използвайте знаменателя на дробата, умножена по 1, за да изравните знаменателя
-
Проблем 3:
15 е новият знаменател.
-
Проблем 4:
14 е новият знаменател.

Стъпка 9. Напишете нов числител и нов знаменател
-
Проблем 3:
14/15 е отговорът 1/3 + 3/5 =?
-
Проблем 4:
6/14 е отговорът 2/7 + 2/14 =?

Стъпка 10. Опростете и намалете дробите
За да опростите дробите, разделете числителя и знаменателя на най -големия общ множител на двете числа.
-
Проблем 3:
14/15 не може да бъде опростен.
-
Проблем 4:
6/14 може да бъде намалено до 3/7 след разделяне на числителя и знаменателя на 2 като най -големия общ коефициент на 6 и 14.
Съвети
- Преди да добавите дроби, уверете се, че знаменателите са еднакви.
- Не събирайте знаменателите. Ако знаменателите са едни и същи, използвайте числото като знаменател след добавянето на дробите.
- Ако искате да добавите дроби с числа, които се състоят от цели числа и дроби, преобразувайте тези числа в дроби и ги съберете съгласно инструкциите по -горе.






