Геометричната средна стойност е друг начин за намиране на средната стойност на набор от числа, който се извършва чрез умножаване на стойностите, преди да се вземат корените, вместо да се добавят стойностите и да се разделят като средно аритметично. Средната геометрична стойност може да се използва за изчисляване на средната норма на възвръщаемост във финансовия анализ или за показване на темповете на растеж на нещо за определен период от време. За да намерите средната геометрия, умножете всички стойности преди вкореняване по, което е общият брой на числата в набора. Можете също така да използвате функцията логаритъм във вашия калкулатор, за да намерите средната геометрия, ако предпочитате.
Стъпка
Метод 1 от 2: Намиране на геометричната средна стойност на набор от стойности
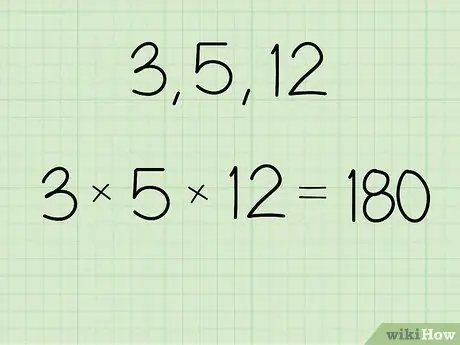
Стъпка 1. Умножете стойността, за която искате да намерите средната геометрия
Можете да използвате калкулатор или да изчислите ръчно, за да получите резултата. Запишете резултатите, за да не забравите.
- Например, ако наборът от числа е 3, 5 и 12, изчислете: (3 x 5 x 12) = 180.
- За друг пример, ако искате да намерите средната геометрия на множеството числа 2 и 18, напишете: (2 x 18) = 36.
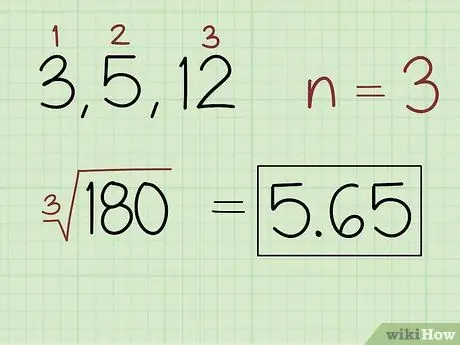
Стъпка 2. Намерете n -ти корен на продукта, където n е броят на стойностите в набора
Пребройте броя на числата в набора, за да получите стойността. Използвайте стойностите, за да посочите корен, който трябва да се използва в продукта. Например, използвайте квадратния корен, ако множеството съдържа 2 числа, кубичния корен, ако множеството съдържа 3 числа и т.н. Използвайте калкулатор, за да решите уравнението и запишете отговора.
- Например за набор от числа 3, 5 и 12 напишете: (180) 5, 65.
- Във втория пример с множеството, съдържащо 2 и 18, напишете: (36) = 6.
Вариант:
Можете също да напишете корена като показател на 1/, ако е по -лесно да пишете на калкулатор. Например за набора от числа 3, 5 и 12 напишете (180)1/3 вместо (180).
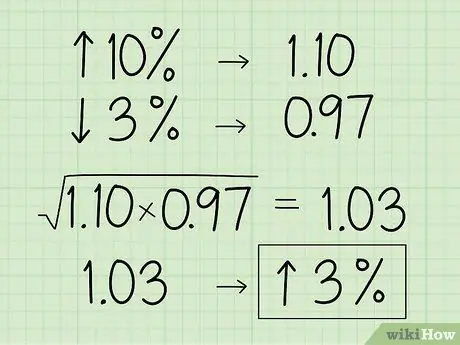
Стъпка 3. Преобразувайте процента в неговия еквивалент на десетичния множител
Ако наборът от числа е записан като увеличение или намаляване на процента, опитайте се да не използвате процентната стойност в средната геометрия, защото резултатите няма да бъдат точни. Ако процентът се увеличи, преместете десетичната запетая с две цифри наляво и добавете 1. Ако процентът намалява, преместете десетичната запетая с 2 цифри наляво и извадете от 1.
- Например, да речем, че искате да намерите геометричната средна стойност на обекта, която се увеличава с 10%, след което намалява с 3%.
- Преобразувайте 10% в десетично число и добавете 1, за да получите 1, 10.
- След това преобразувайте 3% в десетично число и извадете 1, за да получите 0,97.
- Използвайте и двата знака след десетичната запетая, за да намерите геометричната средна стойност: (1, 10 x 0.97) 1.03.
- Преобразувайте числото обратно в процент, като изместите десетичната запетая с 2 цифри надясно и извадите 1, за да получите 3% увеличение на стойността.
Метод 2 от 2: Изчисляване на геометричната средна стойност с помощта на логаритми
Стъпка 1. Добавете логаритмичните стойности за всяко число в набора
Функцията LOG в калкулатора взема основата 10 на число и определя колко трябва да умножите по 10, така че да е равно на числото. Потърсете функцията LOG на калкулатора, която обикновено е от лявата страна на бутона. Щракнете върху бутона LOG и въведете първия номер в комплекта. Въведете „+“, преди да въведете LOG за втория номер. Продължете да отделяте функцията LOG за всяко число със символ плюс, преди да получите сумата.
- Например за набори 7, 9 и 12 въведете log (7) + log (9) + log (12), след което натиснете “=” на калкулатора. Ако функцията е изчислена, числото ще бъде около 2.878521796.
- Можете също така да изчислите всеки логаритъм поотделно, преди да ги добавите всички заедно.
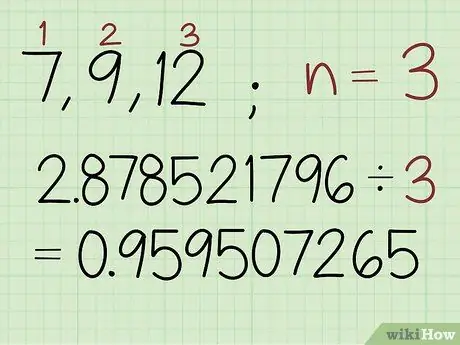
Стъпка 2. Разделете сумата от логаритмичните стойности на броя на числата в множеството
Пребройте броя на стойностите в набора и разделете полученото по -рано число на това число. Резултатът е логаритъмът на средната геометрия.
В този пример има 3 числа в набора, така че въведете: 2, 878521796 /3 0, 959507265
Стъпка 3. Намерете антилога на коефициента, за да определите средната геометрия
Функцията antilog е обратна на функцията LOG на калкулатора и преобразува стойността обратно в база 10. Потърсете символа „10х”На калкулатора, което обикновено е вторична функция на бутона LOG. Натиснете бутона „2 -ри“в горния ляв ъгъл на калкулатора, последван от бутона LOG, за да активирате антилог. Въведете коефициента, намерен в последната стъпка, преди да решите уравнението.
За този пример калкулаторът ще покаже: 10(0, 959507265) ≈ 9, 11.
Съвети
- Не можете да намерите геометричната средна стойност на отрицателните числа.
- Всички множества, които имат 0, ще имат геометрична средна стойност 0.
