- Автор Jason Gerald [email protected].
- Public 2024-01-15 08:09.
- Последно модифициран 2025-01-23 12:07.
Изваждането е просто изваждане на едно число от друго. Лесно е да извадите едно цяло число от друго, но изваждането може да бъде сложно, ако изваждате дроби или десетични знаци. След като разберете изваждането, ще можете да използвате по -сложни математически понятия и да можете да добавяте, умножавате и разделяте числата по -лесно.
Стъпка
Метод 1 от 6: Изваждане на големи цели числа чрез заемане

Стъпка 1. Запишете голямо число
Например, искате да решите 32 - 17. Първо запишете 32.

Стъпка 2. Напишете по -малкото число точно под него
Уверете се, че сте поставили десетките и единичните стойности в правилните колони, така че 3 от 32 да е директно над 1 от 17 и 2 от 32 е директно над 7 от 17.
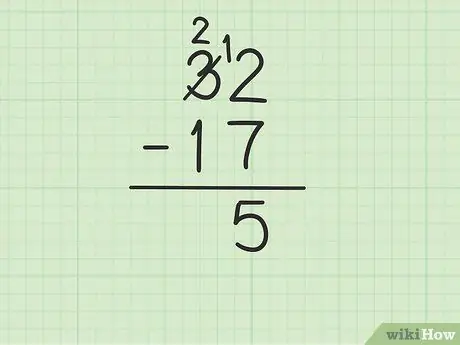
Стъпка 3. Извадете горния номер в колоната с единици от числото в долната част
Това обаче може да се усложни, ако долният номер е по -голям от горния. В този случай 7 е по -голямо от 2. Ето какво трябва да направите:
- Трябва да вземете назаем от номер 3 от 32 (известен също като групиране), за да превърнете 2 в 12.
- Пресечете числото 3 от 32 и го заменете с число 2, докато числото 2 става 12.
- Сега можете да извадите 12 - 7, което е равно на 5. Напишете 5 под двете числа, които изваждате, така че да са в колоната за единици на новия ред.
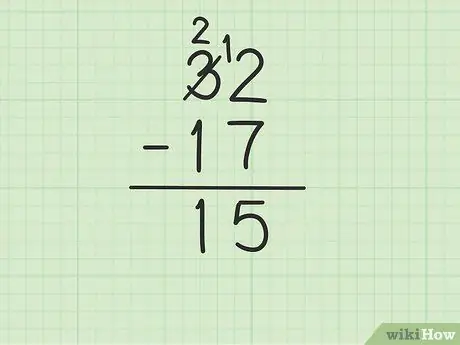
Стъпка 4. Извадете горния номер в колоната десетки от долния номер
Не забравяйте, че 3 е станало 2. Сега извадете 1 от 17 от 2 по-горе, за да получите (2-1) 1. Напишете 1 по-долу, в колоната с десетки, вляво от 5 в колоната с единици. Пишете 15. Тоест 32 - 17 = 15.
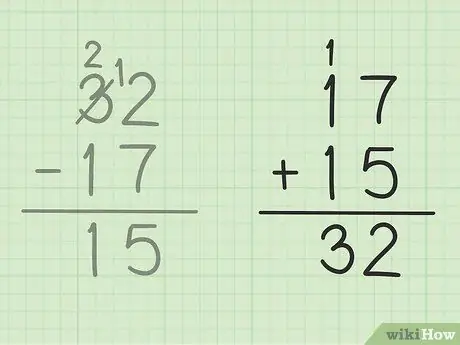
Стъпка 5. Проверете работата си
Ако искате да се уверите, че сте извадили правилно две числа, тогава всичко, което трябва да направите, е да съберете отговора си с по -малкото число, за да направите голямо число. В този проблем трябва да добавите отговора си 15 към по -малкия брой на изваждане, 17. 15 + 17 = 32, така че отговорът ви да е верен. Безопасно!
Метод 2 от 6: Извадете малки цели числа
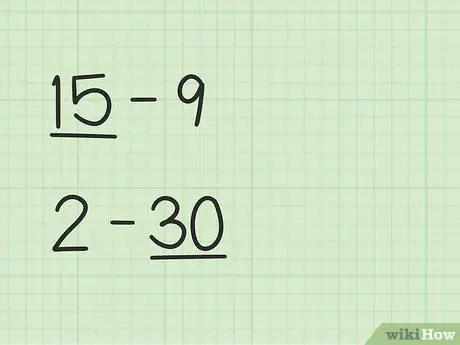
Стъпка 1. Намерете по -голямото число
Проблеми като 15 -9 ще имат различен начин от 2 -30.
- В въпроси 15 - 9 първото число 15 е по -голямо от второто число 9.
- Във въпроси 2 - 30 второто число 30 е по -голямо от първото число, 2.
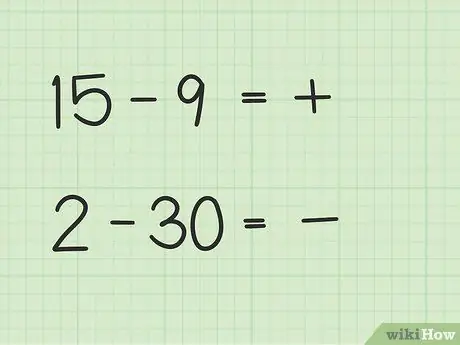
Стъпка 2. Решете дали отговорът ви ще бъде положителен или отрицателен
Ако първото число е по -голямо, отговорът е положителен. Ако второто число е по -голямо, отговорът е отрицателен.
- В първия въпрос 15 - 9 отговорът ви е положителен, тъй като първото число е по -голямо от второто.
- Във втория въпрос, 2 - 30, отговорът ви е отрицателен, тъй като второто число е по -голямо от първото число.
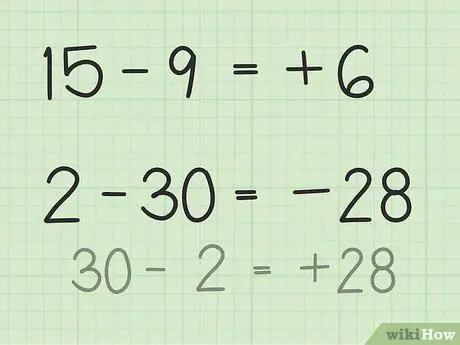
Стъпка 3. Намерете разликата между две числа
За да извадите две числа, трябва да си представите разликата между двете числа и да изчислите числата между тях.
- За въпроси 15 - 9, представете си стак от 15 покер чипа. Изхвърлете 9 чипа и само 6. И така, 15 - 9 = 6. Можете също да си представите числова линия. Помислете за числата от 1 до 15, след това изхвърлете или върнете 9 единици, така че да получите 6.
- За въпроси 2 - 30 най -лесният начин да разрешите това е да обърнете числото и да направите резултата отрицателен след изваждането. И така, 30 - 2 = 28, така че 28 и 30 имат разлика 2. Сега направете резултата отрицателен, защото вече сте определили, че отговорът е отрицателен, защото второто число е по -голямо от първото число. И така, 2 -30 = -28.
Метод 3 от 6: Изваждане на десетични знаци
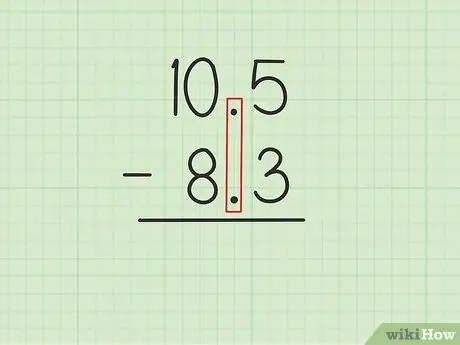
Стъпка 1. Напишете по -голямото число върху по -малкото с подравнени десетични точки
Да предположим, че искате да решите следните задачи: 10, 5 - 8, 3. Напишете 10, 5 върху 8, 3, така че десетичните точки на двете числа да са успоредни., 5 от 10, 5 трябва да са директно над, 3 от 8, 3 и 0 от 10, 5 трябва да са над 8 от 8, 3.
Ако имате проблем, тъй като двете числа нямат един и същ номер след десетичната запетая, напишете 0 на празно място, докато сумата от числата е една и съща. Например проблемът е 5, 32 - 4, 2, можете да го напишете като 5, 32 - 4, 2 0. Това няма да промени стойността на второто число, но ще улесни изваждането на двете числа.

Стъпка 2. Извадете горния номер в колоната десетки от числото по -долу
В този случай трябва да извадите 3 от 5. 5 - 3 = 2, така че трябва да напишете 2 под 3 от 8, 3.
Уверете се, че сте поставили десетична точка в отговора, така че да бъде написана, 2

Стъпка 3. Извадете числото над колоната с единици от числото под него
Трябва да извадите 8 от 0. Заемете 1 от десетичната част, за да промените 0 до 10 и да извадите 10 - 8, за да получите 2. Можете също така да броите 10 - 8, без да заемате, защото няма числа във втората колона с десетки. Напишете отговора под 8, вляво от десетичната запетая.

Стъпка 4. Запишете крайния си резултат
Крайният ви резултат е 2, 2.

Стъпка 5. Проверете работата си
Ако искате да се уверите, че десетичното изваждане е правилно, всичко, което трябва да направите, е да добавите отговора си с по -малкото число, за да направите по -голямото число. 2, 2 + 8, 3 = 10, 5, значи сте приключили.
Метод 4 от 6: Изваждане на дроби

Стъпка 1. Подравнете знаменателя и числителя на дробата
Да предположим, че искате да решите проблеми 13/10 - 3/5. Напишете задачата така, че двата числителя, 13 и 3 и двата знаменателя, 10 и 5 да са един срещу друг. Тези две числа са разделени със знак за изваждане. Това ще ви помогне да визуализирате проблема и да го разрешите по -лесно.

Стъпка 2. Намерете най -малкия общ знаменател
Най -малкият общ знаменател е най -малкото число, което може да бъде разделено на две числа. В този пример трябва да намерите най -малкия общ знаменател, който се дели на 10 и 5. Ще откриете, че 10 е най -малкият общ знаменател и за двете числа, защото 10 се дели на 10 и 5.
Обърнете внимание, че най -малкият общ знаменател на две числа не винаги е едно от тях. Например най -малкият общ знаменател за 3 и 2 е 6, защото 6 е най -малкото число, което може да бъде разделено на две числа
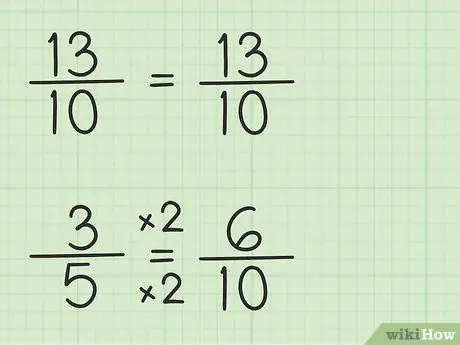
Стъпка 3. Запишете дробите, като използвате същия знаменател
Дробът 13/10 може да бъде записан по същия начин, тъй като знаменателят е 10, най -малкият общ знаменател, който е 10, умножен по 1. Въпреки това, дроб 3/5 трябва да бъде преписан, защото знаменателят е 5, най -малкият общ знаменател, което е 10, умножено по 2. Така че дробът 3/5 трябва да се умножи по 2/2, за да се получи знаменателят 10, така че 3/5 x 2/2 = 6/10. Открили сте еквивалентната дроб. 3/5 е еквивалентно на 6/10, въпреки че 6/10 ви позволява да извадите първото число, 13/10.
Напишете нов въпрос като този: 13/10 - 6/10
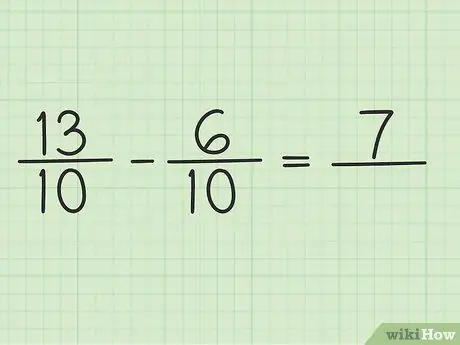
Стъпка 4. Извадете числителя на две числа
Просто извадете 13 - 6, така че резултатът е 7. Не можете да промените знаменателя на дробата.
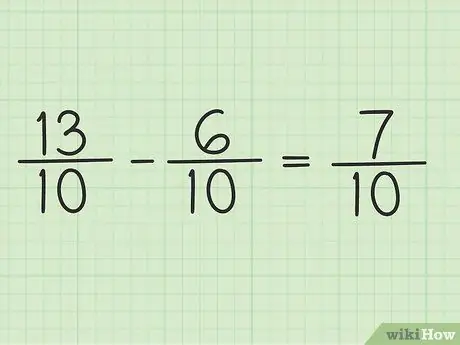
Стъпка 5. Напишете новия числител върху същия знаменател, за да получите крайния резултат
Новият числител е 7. И двете дроби имат знаменател 10. Крайният резултат е 7/10.
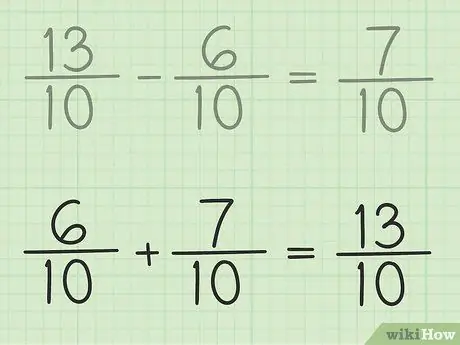
Стъпка 6. Проверете работата си
Ако искате да сте сигурни, че изваждате дробата правилно, просто добавете отговора си и по -малката част, така че резултатът да е по -голяма. 7/10 + 6/10 = 13/10. Готово е.
Метод 5 от 6: Изваждане на дроби от цели числа

Стъпка 1. Запишете проблема
Да предположим например, че искате да решите следния проблем: 5 -. Да го напишеш.
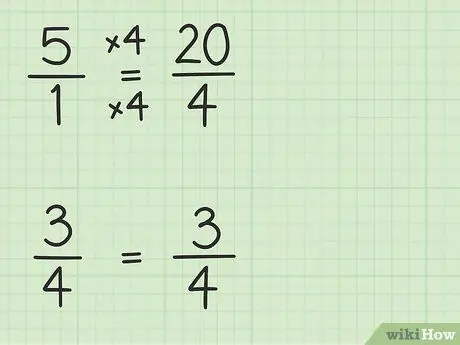
Стъпка 2. Преобразувайте цели числа в дроби, които имат същия знаменател като другите дроби
Ще преобразувате 5 в дроб с знаменател 4, за да можете да извадите две числа. Така че трябва да мислите за 5 като част от 5/1. След това можете да умножите числителя и знаменателя на новата дроб с 4, за да направите знаменателите на двете числа еднакви. Така че 5/1 x 4/4 = 20/4. Тази дроб е равна на 5, но ви позволява да извадите две числа.
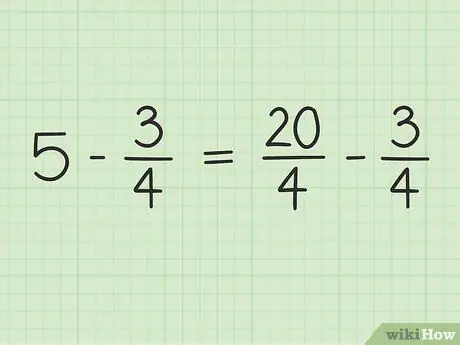
Стъпка 3. Препишете проблема
Новият проблем може да бъде написан така: 20/4 - 3/4.
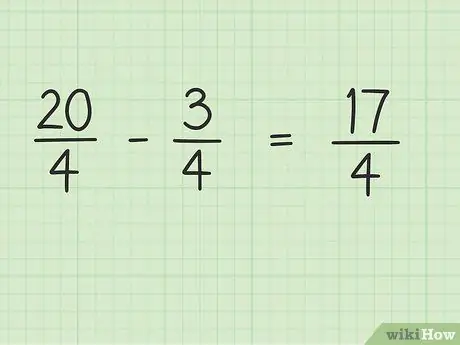
Стъпка 4. Извадете числителя на дробата, докато знаменателят остава същият
Сега просто извадете 20 на 3, за да получите крайния резултат. 20 - 3 = 17, така че 17 е новият числител. Можете да оставите знаменателя същия.
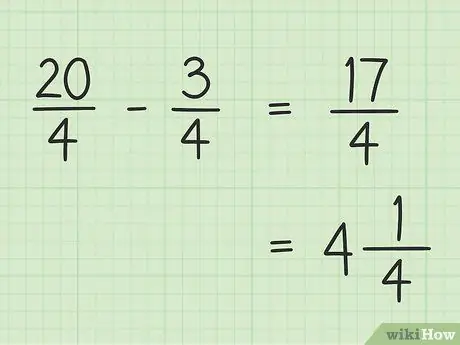
Стъпка 5. Запишете крайния си резултат
Крайният ви резултат е 17/4. Ако искате да го запишете като смесено число, разделете 17 на 4, така че резултатът да е 4, а остатъкът е 1, така че крайният 17/4 да е равен на 4.
Метод 6 от 6: Изваждане на променливи
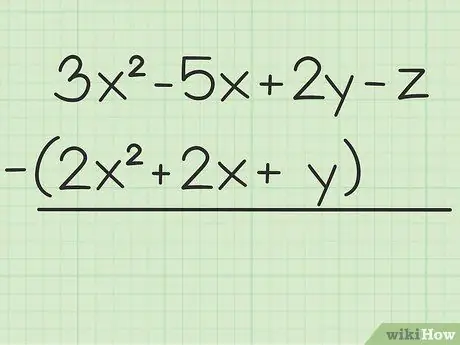
Стъпка 1. Запишете проблема, който искате да разрешите
Например следният въпрос: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Напишете първия набор от променливи над втория.
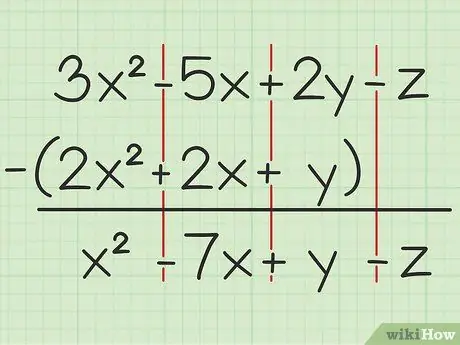
Стъпка 2. Извадете същите променливи
Ако срещнете променлива, можете само да добавяте или изваждате същата променлива и която е написана със същата степен на квадрат. Това означава, че можете да извадите 4x2 от 7x2, но не може да извади 4x от 4y. Така че можете да разбиете проблема така:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
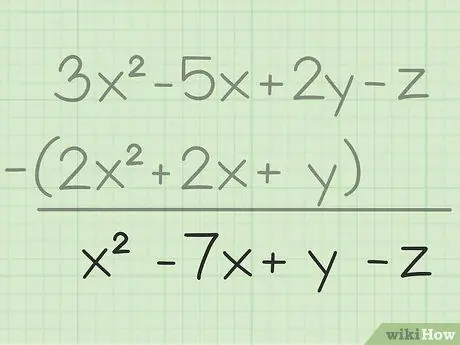
Стъпка 3. Запишете крайния си резултат
Извадили сте едни и същи променливи, всичко, което трябва да направите, е да напишете крайния си резултат, който ще съдържа всички променливи, които сте извадили. Ето крайния резултат:






