- Автор Jason Gerald [email protected].
- Public 2023-12-16 10:56.
- Последно модифициран 2025-01-23 12:07.
За повечето хора дробите са първите сложни изчисления. Понятието за дроби е доста трудно и изисква да научите специални условия, за да го направите. Тъй като дробите имат специални правила за събиране, изваждане, умножение и деление, много хора са объркани за това. Въпреки това, с много практика, всеки може да научи и завърши изчисления, свързани с дроби.
Стъпка
Метод 1 от 5: Разбиране на дробите
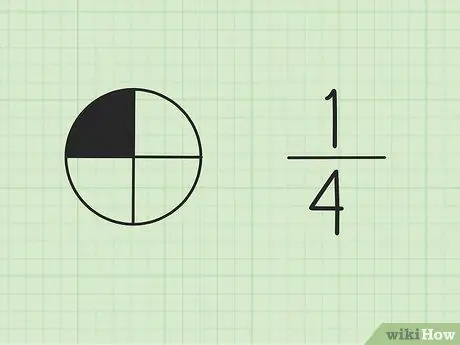
Стъпка 1. Разберете, че дробите са част от едно цяло
Числото в горната част се нарича числител и представлява броя на частите от общата сума. Числото в долната част се нарича знаменател, който представлява общия брой части.
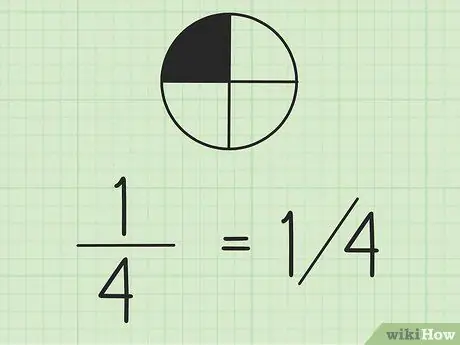
Стъпка 2. Имайте предвид, че можете да пишете дроби с наклонени черти
Числото вляво е числителят, а числото вдясно е знаменателят. Ако работите с дроби на същия ред, добра идея е да напишете числителя над знаменателя.
Например, ако вземете една от четирите филии пица, имате пица. Ако имате 7/3 пици, това означава, че имате две цели пици плюс 1 от 3 филийки пица
Метод 2 от 5: Разлика между смесени и прости дроби

Стъпка 1. Разберете, че смесените числа се състоят от цели числа и дроби, например 2 1/3 или 45 1/2
Обикновено трябва да конвертирате смесени числа в по -проста форма, за да добавяте, изваждате, умножавате или делите.

Стъпка 2. Променете смесеното число, като умножите цялото число по знаменателя във дробата, след което го добавите по числителя
Запишете резултата като числител, докато знаменателят не се променя.
Например, за да преобразувате 2 1/3 в проста дроб, умножете 2 по 3, след това добавете 1 и получете 7/3

Стъпка 3. Преобразувайте прости дроби в смесени числа, като разделите числителя на знаменателя
Целият резултат от делението се записва като цяло число, а остатъкът от делението се записва като числител на дробата. Знаменателят не се променя.
Например, за да преобразувате 7/3 в смесено число, разделете 7 на 3, за да получите 2 с остатък от 1. Така че смесеното число е 2 1/3. Простите дроби могат да бъдат преобразувани само в смесени числа, ако числителят е по -голям от знаменателя
Метод 3 от 5: Добавяне и изваждане на дроби
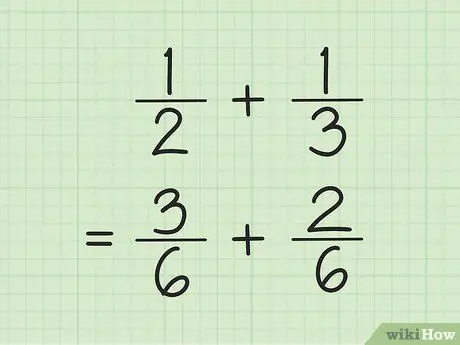
Стъпка 1. Намерете общ знаменател за добавяне и изваждане на дроби
Трикът, умножете числата в знаменателя, след това умножете всеки числител по числото, използвано за намиране на знаменателя. Понякога можете да намерите LCM (най -малко общо кратно) за знаменателя, като умножите знаменателите един с друг.
Например, за да добавите и 1/3, първо намерете LCM (най -малкото общо кратно) на двата знаменателя, като се умножите един друг. По този начин умножавате 2 и 3, за да получите LCM 6. Умножете 1 по 3, за да получите 3 като нов числител на първата дроб. Умножете 1 по 2, за да получите 2 като нов числител на втората дроб. Вашите нови дроби са 3/6 и 2/6
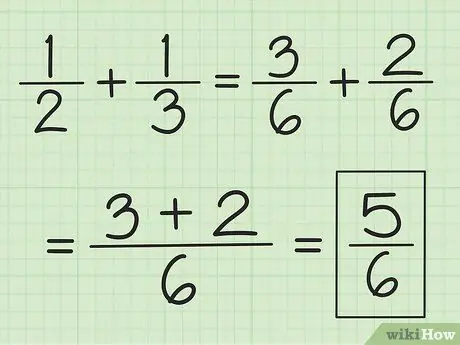
Стъпка 2. Добавете двата числителя заедно и не променяйте знаменателя
Например 3/6 плюс 2/6 е 5/6, а 2/6 плюс 1/6 е 3/6
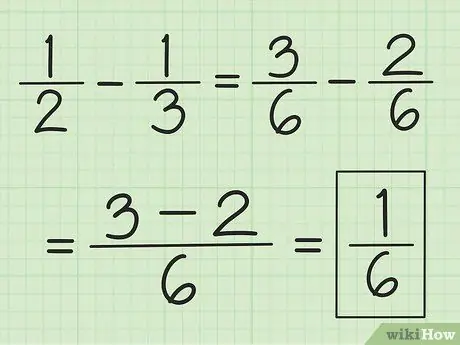
Стъпка 3. Използвайте подобна техника за изваждане
Първо намерете LCM на знаменателите, но вместо да ги събирате, извадете номера на първия числител с номера на втория.
Например, за да извадите 1/3 от 1/2, първо променете дробите на 3/6 и 2/6, след това извадете 3 на 2, за да получите 1. Това води до 1/6
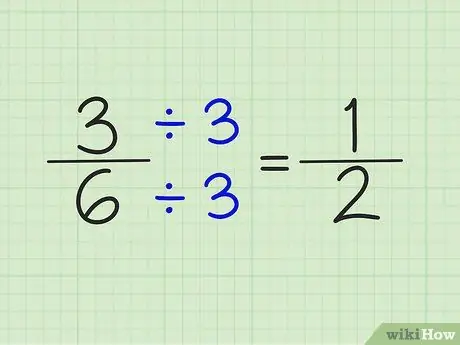
Стъпка 4. Опростете дробите, като разделите числителя и знаменателя на едно и също число
Например, числото 5/6 не може да бъде опростено. Въпреки това, 3/6 може да бъде опростено чрез разделяне на числителя и знаменателя на числото 3. Резултатът е част от 1/2

Стъпка 5. Преобразувайте дробата в смесено число, ако числителят е по -голям от знаменателя
Метод 4 от 5: Умножете и разделете дроби
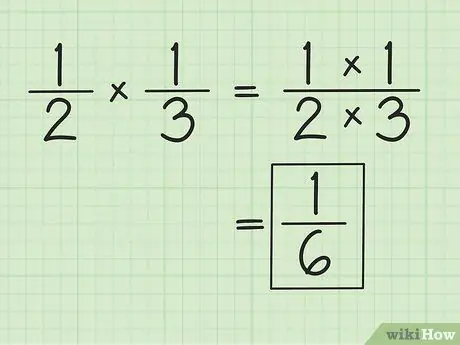
Стъпка 1. Умножете числителя и знаменателя отделно, за да умножите дроби
Например при умножение и 1/3 резултатът е 1/6 (1 по 1 и 2 по 3). Не е необходимо да съпоставяте знаменателите, когато умножавате дроби. Опростете или променете получените резултати, ако е необходимо
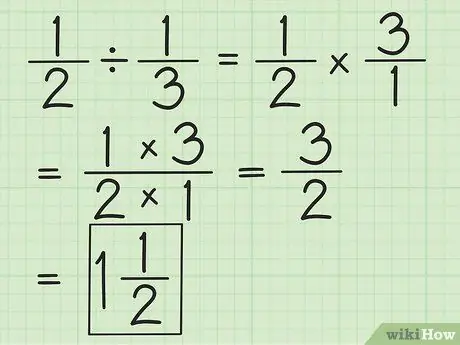
Стъпка 2. Разделете две дроби, като обърнете втората дроб, след което умножете и двете
Например, ако искате да разделите 1/2 на 1/3, първо обърнете втората дроб на 3/1. Умножете по 3/1 и получете 3/2. Опростете дробите или конвертирайте в смесени числа, ако е възможно
Метод 5 от 5: Работа със сложни дроби
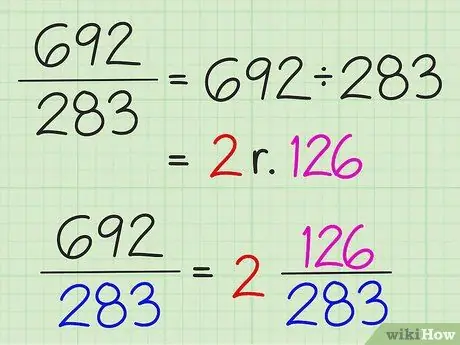
Стъпка 1. Работете по всички дроби по същия начин, дори ако проблемът изглежда много сложен
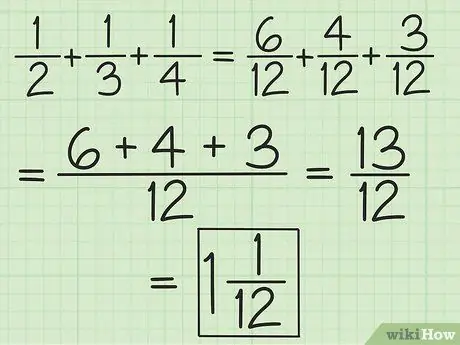
Стъпка 2. Съпоставете знаменателите за всички дроби или работете по двойки, започвайки отляво надясно, за да добавяте и изваждате повече от две дроби
Например, за да добавите 1/2, 1/3 и 1/4, можете да ги промените на 6/12, 4/12 и 3/12, за да получите 13/12, или можете да добавите 3/6 и 2 /6, така че получавате 5/6, след това добавете 5/6 и 1/4 (изравнете знаменателите, така че втората дроб да стане 3/12), за да получите 13/12 (10/12 плюс 3/12). Преобразувайте го в смесено число, което е 1 1/12
Съвети
- Не забравяйте, че сте научили доста математика. Математиката е като език, който можете да произнасяте свободно и сега се опитвате да се научите да го четете и пишете.
- Не забравяйте винаги да опростявате крайния резултат от изчислението си, независимо дали проблемът ви е под формата на обикновена дроб, смесено число или сложна дроб.






